A generalised version of the Hammett equation has been developed by researchers in Switzerland. Anatole von Lilienfeld and his team at the University of Basel used a statistical method to optimise two parameters that determine the Hammett equation, allowing the relationship between free energy and substituents to be determined with higher accuracy. The new version will allow users to predict activation energies in non-aromatic molecules with multiple substituents.
Louis Plack Hammett first developed the Hammett equation in the 1930s. It relates structure and reactivity in substituted aromatic compounds and allows physical organic chemists to investigate reaction pathways and determine the influence of substituents and process variables such as solvent, temperature and mechanism. It is a linear free-energy relationship and relates reaction rates and equilibrium constants to each other.
Despite its widespread use, the method is not without limitations and there have been many attempts to expand the equation to encompass other effects and different systems. Von Lilienfeld and his team saw the value in being able to use the Hammett equation to reliably predict reaction outcomes in other systems. The team identified three main limitations of the approach: ‘the focus on single substituents, the difficulty to obtain a consistent set of Hammett coefficients and the restriction to free energy differences.’
They set about addressing these limitations to make the equation more robust and transferrable. The new model uses the Thiel-Sen regressor, a method for fitting a line to points. It fits to the median of all possible slopes, which is less susceptible to outliers than the mean and improves accuracy. Additionally, they calculated the entire set of reaction constants, ρ, at once, removing dependence on the choice of reference reaction. The equation is then inverted and the substituent constant, σ, determined by averaging the results across all reactions. Their new version allows for multiple substituents and non-aromatic scaffolds, thereby making it applicable to a wider range of reactions. ‘The original Hammett approach suffers from severe bias due to the arbitrary selection of reference reaction and substituents,’ says von Lilienfeld. ‘This can lead to trends among prediction errors reminiscent of overfitting.’ They included all available training data in the regression and their benchmarking demonstrated that the new technique reduced outlier predictions.
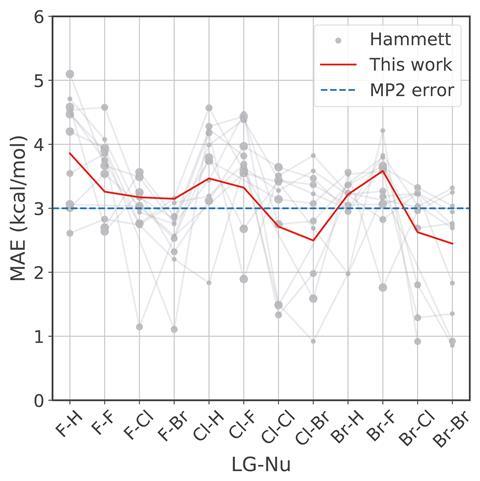
Compared with predictions using the original Hammett method, the new method is more reliable when predicting rate constants and lowered the mean absolute error for predicting activation energy. Von Lilienfeld says an additional benefit to improving the predictive power is ‘a decomposition of the substituent constants that gives more chemical interpretability to the model’, meaning the model can help guide rational design of chemical compounds.
Clémence Corminboeuf, a computational and theoretical chemistry expert at the Swiss Federal Institute of Technology Lausanne (EPFL), says ‘the proposed framework is robust and performs surprisingly well, especially when considering that the model remains a linear scaling relationship.’ She adds that ‘a nice outcome of this work is the derivation of a single, well-defined set of Hammett’s coefficients and the ability of treating multiple substituents in the equation.’
Von Lilienfeld says that ‘a particular challenge was the scarcity of openly accessible, machine-readable, consistent reference data to train and evaluate models or to test theories.’ They overcame this by using experimental literature results of rate constants for benchmarking and by using a synthetic data set of activation energies. Future work from the team will integrate Hammett’s ansatz into machine learning models and investigate if they can apply it to other systems and properties.
References
This article is open access
M Bragato, G F von Rudorff and O A von Lilienfeld, Chem. Sci., 2020, DOI: 10.1039/d0sc04235h


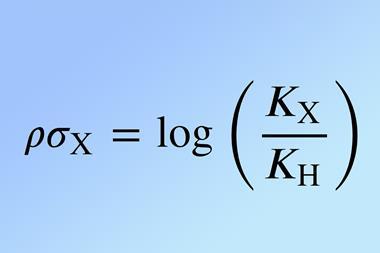









No comments yet