Subtle forces yield profound effects on heavy element bonding

Using theoretical calculations, researchers in the US and Japan, have cast a spotlight on the vital role that subtle, and previously overlooked, dispersion forces play in stabilising p-block heavy element bonding.¹

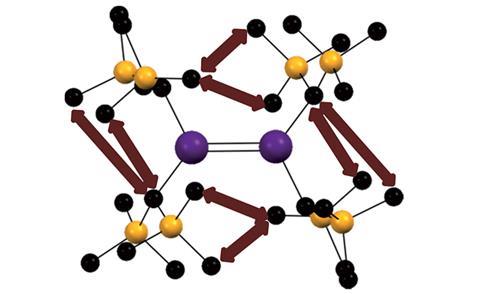
It was once thought that heavy elements could not form multiple bonds, but landmark work by inorganic chemists such as Mike Lappert² in the 1970s blew the doors off this notion and opened up a whole new world for main group chemistry. Since then, the study of heavier p-block elements with multiple bonds has remained a topic of broad interest and exciting discoveries. One key development was that sterically large ligands block decomposition and stabilise bonds. However, questions over how and why these compounds remain stable continue to be debated.    

Inspired by recent work highlighting the importance of London dispersion forces for carbon–carbon bonding,³Shigeru Nagase from Kyoto University and Phil Power from the University of California Davis, and co-workers Jing-Dong Guo and David Liptrot returned to the origins of this topic, describing density functional theory (DFT) calculations modified for dispersion effects by the method of Grimme⁴ on main group element alkene analogues, including Lappert’s original [E(CH{SiMe₃}₂)]₂ dimers (E = Ge, Sn, Pb). Their computational analysis shows that subtle dispersion force attraction between ligands forms the largest driving force towards dimerisation, and stabilisation of the E–E bonds in these compounds. Calculations were run with and without dispersion force modification and those without revealed that E–E bonding energies were insufficient to cause dimer formation under ambient conditions. Previous work had focused almost exclusively on the details of the interaction between the heavy elements, i.e. the orbitals involved, their overlap, bonding character and even the energetics of multiple bond formation.   

Yet, despite dispersion forces being well known in other areas, their importance in the stabilisation of molecular species has taken a long time to be realised, comments Power. ‘I was just as oblivious to it as most others. It’s only recently that several the experimental results have suggested that something other than the usual forces, such as overlap and energy levels, matter in their bonding.’

Christine Thomas, an inorganic chemist at Brandeis University in the US, says the study highlights the importance of including dispersion corrections in DFT calculations to accurately model metal–metal binding energies. ‘Subtle-to-modest differences in calculated thermodynamic parameters with different computational methods are common, but the 20–30kcal/mol difference in binding energies when dispersion is included in the calculations is huge.’

Thomas adds that ‘it’ll be interesting to see whether similar dispersion effects are at play in other element–element multiply bonded systems throughout the heavier main group and transition metal series.’

This is Power’s ultimate aim, with this work laying out a framework for designing molecules from scratch with enhanced dispersion forces. As Power explains ‘there are many classes of compound that are currently unknown, for example, homoleptic transition metal dialkyls are very rare. By that I mean ones with no other ligands, only the alkyl ligands.’ He also hopes that such forces might be used to control disproportionation and generally allow access to hitherto unknown compounds in inorganic and organometallic chemistry.