Sorel’s plates

Students are always asking for model answers. But at some point one has to move beyond such things; research, and indeed real life, requires us to act without someone else knowing the correct answer. This is amply demonstrated by the history of distillation. This ancient technique went from an empirical art to a real science in a tentative process, with false starts and dead ends, largely because of the absence of the key idea of dynamic equilibrium – a model answer we now take for granted.

In the early 19th century, many formerly artisinal processes were scaled up and intensified as part of the Industrial Revolution. Distillation was well-established as a technique, and production of various kinds of hooch was growing steadily. This involved heating a fermented mash at the bottom of a pot still to separate the more volatile ‘spirit’ from the heavier aqueous ‘phlegm’.

As the Industrial Revolution gathered pace, scientific ideas about heat began to be applied to distillation. Increasingly complicated still systems were developed to improve the efficiency (and reduce the costs) of distillation. In these new stills, the vapour from the still pot passed through a series of chambers where it bubbled through condensed liquid, which drained back into the pot. The latent heat of condensation maintained the temperature of the returning ‘phlegm’. But these were batch stills; once the alcohol was exhausted, the still was cooled, drained and reloaded.

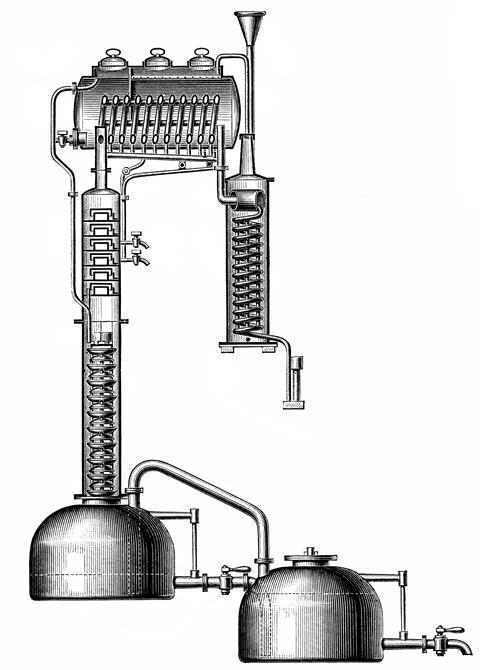
The many incremental improvements in the technology were combined into a revolutionary still developed between 1813 and 1818 by a French distiller, Joseph Cellier-Blumenthal, working in what is today Belgium. Rather than putting the mash in the bottom of the still, Cellier-Blumenthal used the still-pot to generate steam. The vapour rose through a dephlegmator – a cylindrical column equipped with a series of perforated trays or plates – until it reached a pair of condensers. There the fermented mash, known as the ‘wash’, cooled the vapour. The heated wash then fell step by step down the trays of the dephlegmator, while the alcohol joined the upward current of vapour; it was the first example of counter-current separation.

The result was a phenomenally economical still that could be run 24 hours a day, fed by a continuous stream of mash. Cellier-Blumenthal would soon modify the trays to incorporate lips and caps to cause the vapour to bubble through the trays. These were the progenitors of the vast fractionators that sit at the heart of oil refineries today.

All of these developments took place empirically, with only the most rudimentary ideas of the mechanism by which distillation took place. A conception that seems utterly obvious to us – equilibrium – was still being debated. The law of mass action was only developed, in several stages, during the 1860s. But the original reports made so little impact that Henricus van ’t Hoff rediscovered it independently 10 years later. Instead, chemists and distillers had vague ideas about the vapour being ‘washed’ by the phlegm.

The first mathematical model of distillation would not appear until about 1890 when Ernest Sorel began to think about the process quantitatively. Sorel had studied at the École Polytechnique, the elite university in Paris famous for its rigorous mathematical foundation. Wounded in 1869 in the Franco-Prussian war, Sorel became something of a jobbing chemist and engineer, acting often as a trouble-shooter and developing a reputation as a clear thinker and good problem-solver.

When he joined the still-maker Savalle around 1889 he had already started publishing his ideas about distillation. Sorel’s treatment focused on each bubble plate in the still, calculating the vapour–liquid equilibria by taking into account both the mass balance and the conservation of energy. This led to a rather long-winded and tedious stepwise calculation of the equilibria through the column. After submitting papers to the French academy, he wrote a short book La Réctification de l’Alcool that laid out the theoretical principles for a full understanding of alcohol distillation and gave detailed design guidelines.

Sorel’s later work on alcohol in combustion engines ended with his sudden death at age 54. In his eulogy Henri Le Chatelier raged at the early loss of a man of such brilliance. But Sorel’s key idea, the vapour-liquid equilibrium at each plate, would be taken up by Warren Lewis at the Massachusetts Institute of Technology, US. Lewis streamlined Sorel’s mathematics and added graphical shortcuts; in 1922, William Peters at Dupont described a general criterion of still efficiency, the ‘height equivalent to a theoretical plate’, and this would lead to the even more visual McCabe–Thiele plots. In a strange sort of way, over the course of a century the physical plates of Cellier-Blumenthal dematerialised into something virtual but even more widely applicable. It shows that you never can tell what the model answer should be until you actually work through the question.