The art of changing phases

150 years ago, James Clerk Maxwell gave a public lecture entitled ‘Molecules’, which was published in Nature that same year.¹ Maxwell’s molecules were very much a physicist’s vision: he called them ‘the smallest portion of a particular substance’ and regarded them as ‘incapable of growth or decay, of generation or destruction’. They were also the devout Scottish Presbyterian’s version: ‘essential constituents of the image of Him Who in the beginning created … the heaven and the earth’.

‘The study of molecules [has] opened up new views of nature,’ Maxwell claimed. That was partly thanks to his own kinetic theory of gases, presented in 1867. But the prime reason why this year is indeed the 150th anniversary of a revolution in statistical mechanics and our understanding of the phases of matter is a treatise that Maxwell read that same year and which influenced him deeply, written by Johannes Diderik van der Waals.

Maxwell’s kinetic theory had explained the long-known relationships between pressure, temperature and volume on the basis of how the velocities of the microscopic molecules were statistically distributed. In his lecture, Maxwell acknowledged that his theory had been ‘greatly developed and improved’ by Ludwig Boltzmann, who in 1872 showed that the bell-curve distribution of velocities simply assumed by Maxwell was that to which any other initial distribution would inevitably converge at equilibrium.

Attractive ideas

In this theory, the molecules were assumed to be hard spheres, interacting not at all until they touch and undergo elastic collisions. In a paper in Nature in 1874, Maxwell offered a more sophisticated view of this interaction: ‘We have evidence that the molecules of gases attract each other at a certain small distance, but when they are brought still nearer they repel each other.’² The idea of an oscillatory molecular attraction and repulsion was proposed in the 18th century by Roger Boscovich, but the hard evidence Maxwell alluded to was provided by van der Waals’ doctoral thesis presented to the University of Leiden in 1873, and which Maxwell immediately reviewed for Nature.

Formation of the dense liquid state from a gas implied that there must be some attractive force between molecules

The thesis was stimulated by experiments of chemist Thomas Andrews in Belfast in the 1860s, showing that liquids and gases could be interconverted by manipulating temperature and pressure without going through the abrupt phase transitions of evaporation and condensation. Van der Waals presented the first explanation for (as his title put it) this ‘continuity of the gaseous and liquid states’. Formation of the dense liquid state from a gas implied that there must be some attractive force between molecules. Van der Waals incorporated such a force (which now bears his name) into a modified ‘equation of state’ relating the pressure, volume and temperature of the fluid. The short-range repulsion of molecules, meanwhile, was included as a term that accounted for the finite volume occupied by the molecules themselves.

Nobel work

This new equation of state implied that the relation between pressure and volume offers two possible states – one dense, one rarefied – but that these differ ever less in density as the temperature is raised, until ultimately they coalesce into a single state. This corresponds to the critical point identified by Andrews for carbon dioxide. In this way, van der Waals unified the Maxwell-Boltzmann view of gases with a theory of liquids that acknowledged intermolecular attraction, a notion used previously by Pierre-Simon Laplace and Thomas Young to understand capillarity. It later became clear that van der Waals’ theory was the first ‘mean field theory’ of phase transitions and critical phenomena, in which the range of particle interactions is essentially assumed to be infinite. From it flowed many ideas central to modern many-body physics, which have found their way into studies of magnetism, superconductivity, quantum chromodynamics (the theory of quarks in nucleons) and more. A remarkable amount of this framework was already inherent in van der Waals’ thesis. When chemical physicist Ben Widom asked in a paper of 1999 ’What do we know that van der Waals did not?’, he concluded: ‘Not very much.’³ In 1910 the Dutchman was awarded the physics (but should it have been chemistry?) Nobel prize.

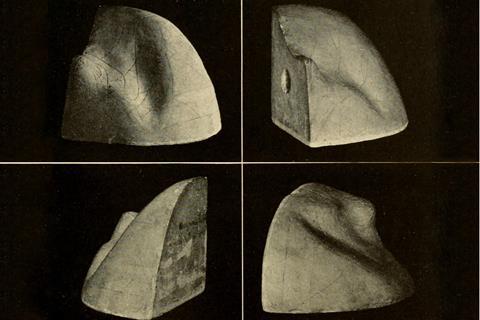
One question van der Waals couldn’t answer was how to determine the point on his equation of state curve where a liquid switched to gas. Maxwell solved that problem in 1875 with his ‘equal areas’ rule for the loops of the curve defined by the transition point.⁴ There he paid testament to the explanation of the equilibrium transition in terms of free energies of the two states provided in another landmark 1873 paper, by the American chemist Josiah Willard Gibbs.⁵ Gibbs’ work implied that the full P, V, T (in fact the energy–entropy–volume) relationship of liquids and gases was defined by a curving surface in three dimensions. Maxwell was so entranced by it that in 1874 he had a plaster cast made and sent it to Gibbs at Yale, where it remains on display to this day.

This article was updated on 7 June to note that the P, V, T relationship was first described by Gibbs as a relationship between energy, entropy and volume.