How many physical scientists can really dance?

How many physical scientists can really dance? Most people would argue that the number is fairly small on the grounds that most scientists spend more time reading and experimenting than practising fancy steps on the dance floor. But if you think dance to be of little relevance to our understanding of the universe, think again. Are not all oscillations just organised, rhythmic motions of matter?
A scientist who probably didn’t dance, or at least not much, was Louis-Georges Gouy (pronounced Gooey). He was born in the small spa town of Vals, south west of Lyon in France, not far from the spectacular gorges of the Ardèche river. Nothing is known of his family or his schooling, but he studied at the École Polytechnique near Paris under Jules Jamin and became a close friend of Pierre Curie’s. An outspoken and confident figure as a student, he irritated Jamin by dismissing his theories of soap bubbles. On graduation, he and Pierre Curie moved to the Sorbonne (also in Paris) where they became assistants to the experimental physicist Pierre Desains, who had proven that radiant heat was a transverse wave like light.
In 1879 Gouy presented a thesis on flame photometry, which combined his theoretical and practical skills. As an assistant, Gouy also taught physics but was criticised by inspectors for his rather stodgy lectures. Even as a youth, Gouy didn’t do flashy.
In the 1880s Gouy made a number of important contributions to optics that demonstrated how the speed and phase of light waves depended on the nature of the medium and on their shape. It was beautiful physics, soon confirmed by English physicist Lord Rayleigh, which would be rediscovered a century later by laser physicists and NMR spectroscopists.
In 1883, Gouy accepted a professorship at the University in Lyon. His interests were wide and varied and he seemed to have picked and chosen projects that took his fancy. He continued to work in optics, using interferometry to investigate the diffusion of salts. By splitting a beam of light and passing it through different parts of a capillary tube before they were recombined Gouy had, in the interference fringes, a probe of refractive index of exquisite sensitivity. The Gouy-Jamin interferometer continues to be mentioned in the context of ultracentrifugation of biological molecules. His interests in thermodynamics led him to explore osmosis, dielectrics, electrocapillarity and interactions at surfaces.
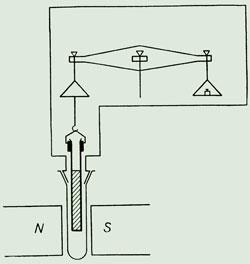
But Gouy also had interests in magnetism. In 1888, the German physicist Georg Quincke reported that the meniscus of a liquid in a capillary moved under the influence of a magnetic field. He showed that pressure changes could be related to the sample’s magnetic susceptibility. Intrigued, in 1889 Gouy derived an expression for the interaction of a cylinder of material in a uniform magnetic field, showing how the force would be proportional to the volume susceptibility. He proposed that measurements be made by weighing tubes of material hanging inside a magnetic field from a balance. He never took the method forward, but because of its cheapness and simplicity others did, and it became a standard way to measure magnetic susceptibility.

Gouy was also investigating Brownian motion, the erratic motion of colloidal particles suspended in liquids, an example of perpetual motion, which some argued must be a contravention of the second law of thermodynamics. Gouy showed how the phenomenon - unaffected by light, temperature, concentration, vibrations, or magnetic fields - depended only on the size of particle and the viscosity of the liquid. Brownian motion, he concluded ’is unique in revealing the internal restlessness of matter’. The motion ’must be of cardinal importance for molecular physics’. But without a theoretical framework, Gouy moved on. In 1905 and 1906, Albert Einstein and Polish physicist Marian Smoluchowski - both oblivious to Gouy’s work - independently published statistical treatments of the motion. In 1913, Jean Perrin plotted the dance of the motes, confirming the existence of atoms.
Who knows what the modest Gouy thought? An eloquent proponent of atomism, and a powerful inspiration for a generation of Lyon chemists including Victor Grignard, Gouy was fundamentally conservative. When he retired from Lyon he returned to the town of his birth where he died in 1926 - the year that Perrin was awarded the Nobel prize.
We will never know whether Gouy could dance. But the restless dance of molecules, which he had studied so carefully, was echoed in the riotous premiere of Stravinsky’s Rite of Spring in 1913. While his wave packets now choreograph our NMR and laser experiments.
So don’t just sit there. Turn up the music. And dance.
References
L-G Gouy, Sur l’énergie potentielle magnétique et la mesure des coefficients d’aimantation,C. R. Acad. Sci., 1889, T109, 935











No comments yet