Beam me up

No comments

It sounds fantastical, but Philip Ball explains how teleportation may one day make it out of the realms of science fiction and become a reality.

Chemists are used to making copies. They can use sequences of chemical reactions to replicate complicated natural molecules atom for atom. But chemical synthesis doesn’t offer any real control at the quantum level - one can’t use it to specify the exact quantum state of a molecule. So copying a molecule using chemistry alone produces the equivalent of a bad forgery or a fuzzy photocopy - it looks the same until you peer closely. Earlier this year, however, teams of scientists in Austria and the US figured out how to make much more accurate quantum copies of individual atoms.

In fact, copying isn’t quite the right word for it. In order to reproduce the quantum state of one atom in a second atom, the original has to be destroyed. This is unavoidable - it is enforced by the laws of quantum mechanics, which stipulate that you can’t ’clone’ a quantum state. In principle, however, the ’copy’ can be indistinguishable from the original, and the process can take place at the speed of light. So it’s as if the original atom vanishes at one place and reappears elsewhere, sent there at light speed. In other words, this is a form of teleportation.

Rainer Blatt and colleagues at the University of Innsbruck, and David Wineland’s team at the National Institute of Standards and Technology (NIST) in Boulder, Colorado, have independently transferred the quantum state of one ion to another. The transfer isn’t yet perfect - the copy is only about three-quarters identical to the original - but it’s significantly better than what any ’copying’ process can achieve without quantum teleportation. And there will surely be better to come.

Quantum teleportation has been demonstrated before, but only with photons. This could be useful for quantum information processing - for example, for sending information reliably and securely between distant locations. But it is a rather ethereal phenomenon. The new demonstration that it can work for atoms too brings quantum teleportation solidly into the material world, and allows researchers to start speculating a little more freely. Might one teleport a molecule, for example? Or an entire group of molecules? In fact, what about the kind of teleportation favoured by science fiction writers and made famous by the Star Trek series, where humans are beamed intact through the ether from a spaceship to a planet’s surface? Nothing of that sort is likely to be possible in the foreseeable future - but we can take heart from knowing that there’s nothing in the laws of physics that seems to prohibit it in principle.

Using quantum mechanics for teleportation is a way of getting around the limitations that the quantum world imposes on making copies. Imagine a copying process in which the position and state of every atom in an object is laboriously measured and then this information is sent to another place where a replica is assembled with exactly the same specifications. It would be a hugely difficult task for a macroscopic object; but mightn’t it just be feasible for, say, a single molecule?

No it isn’t, because Heisenberg’s uncertainty principle restricts the amount of information we can gather about a quantum object. It tells us that we can never know everything, appearing to imply that we can’t ever make a perfect replica. What’s more, the more accurately we try to look, the more we have to probe the object, and so the more it is disturbed. Well before we can gather enough information to make even a near-perfect replica, the object has been so perturbed that it doesn’t look the same anyway. That seems to scupper the whole idea.

In 1993, physicist Charles Bennett of IBM’s research laboratories in Yorktown Heights, New York, US, found an ingenious solution to the problem. He realised that the information specifying the state of a quantum object - a particle, say, which could be a photon or an atom or even a group of atoms - can be divided into two parts, which might be loosely called classical and quantum. The classical information is stuff one can find out by making measurements on the particle. The quantum information is all the other stuff, ’hidden’ from measurement by the uncertainty principle.

Bennett and his colleagues devised a scheme for transferring the quantum information from one particle (A) onto another particle (B) without having to actually measure it. So one never gets to know what this information is, and as a result one doesn’t fall foul of the uncertainty principle - yet all the same, one can ensure that the information is duplicated in particle B. The classical information about A, meanwhile, is measured by conventional means and then transmitted to the location of B, where it can be ’installed’ in B to complete the copying procedure.

But making a measurement on A inevitably perturbs its original state: in other words, the quantum state of A is scrambled by the process of extracting the classical information. So in effect the original particle is ’destroyed’ at one place and ’recreated’ elsewhere. The trick is to get the quantum information from A to B without them ever having to interact.

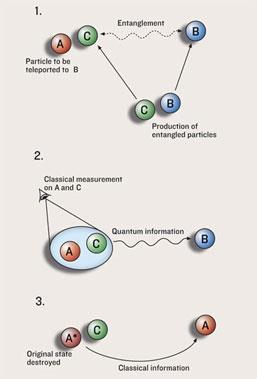
That is done with a third, ’messenger’ particle - call it C. The key is to prepare B and C in a so-called entangled state: a peculiar quantum state in which the two particles are correlated. The entangled state is a superposition of quantum states: an undefined situation in which B and C are not in precise quantum states but have only certain probabilities of being in one state or another. The particles adopt definite states only if they are probed by some measuring apparatus. Such a measurement destroys the entangled state.

While they are entangled, the states of B and C are inter-related, so that a measurement on one of them simultaneously determines the quantum state of them both. Even if the two entangled particles have drifted light years apart, measuring B automatically defines the state of C. In effect, entanglement sets up a communication channel that can be used to instantaneously transmit an influence from one particle to the other.

How teleportation works: particle A is to be teleported onto particle B, mediated by particle C. 1) B and C make an entangled pair. 2) Simultaneous classical measurement of A and C extracts partial information about them, at the same time changing their quantum states and transferring quantum information about A, via entanglement between B and C, onto B. 3) Classical information about the original particle A is transmitted conventionally to B at the receiving station, completing the conversion of B into a replica of A

Relativistically speaking

Albert Einstein was one of the first to realise that quantum mechanics seemed to permit this instantaneous ’action at a distance’, which he called ’spooky’. Despite appearances, it doesn’t by itself violate Einstein’s famous relativistic dictum that nothing can travel faster than light, because relativity’s speed limit applies only to meaningful information - that is, to ’signals’ that we can read. Entanglement can’t be used to convey accessible information.

All the same, Einstein could not believe the world was really this strange. The paper in which he introduced the notion of entanglement, cowritten with his students Boris Podolsky and Nathan Rosen in 1935, was intended as a demonstration that quantum mechanics was somehow incomplete. It described a thought experiment for preparing pairs of entangled particles. In the 1960s, Irish physicist John Bell argued that a link - so-called EPR correlations - between two entangled particles should indeed exist. This was confirmed by experiments on light in the 1980s.

Entanglement supplies the link that allows ’hidden’ quantum information to zip between the two particles A and B in a teleportation experiment. It works like this. The target and messenger particles, B and C, are prepared in an entangled state, and C is sent to the ’sending station’, where particle A is waiting to be teleported. The sender makes a measurement on A and C together to gather the ’classical’ part of the information on A that she wants to transfer to B. The clever aspect is that, by making this measurement on the two particles together, the missing quantum information on A, which cannot be measured directly, doesn’t get lost, but instead gets transferred, via the entanglement link, from C to B. Even though A and C aren’t themselves entangled, probing them both together means that the quantum state of A affects the way that C and B interact.

The classical information from this measurement can then be sent along by conventional means - beamed by radio signal or whatever - and programmed into B. In this way, the exact state of A gets recreated in B (see figure, left).

Quantum teleportation was first achieved experimentally four years after Bennett proposed it. Two groups succeeded almost simultaneously in teleporting a photon over a short distance in the laboratory. At the University of Innsbruck, Anton Zeilinger and coworkers used Bennett’s original scheme, but they had only limited control over the measurement of photons A and C: in their experiment, these two photons were fired at the measuring device independently, so that only occasionally did they happen to arrive together. In those cases the measurement could be made on both particles simultaneously, so that successful teleportation occurred. In Italy, Francesco De Martini and coworkers at the University of Rome ’La Sapienza’ used a slightly different approach: instead of having separate particles A and C, they measured two different properties (the direction and polarisation) of a single photon, with just the polarisation being entangled with the target photon B. This gave a much higher success rate for teleportation.

Since then, there have been several demonstrations of teleportation with photons, but they suffer from the same drawback that one can’t control which events will lead to teleportation and which will not. Instead, one has to simply measure all the photons and then retrospectively separate the successes from the failures. It is hard to make any practical use of such teleportation when you don’t know if it is going to work or not.

Trapping atoms

The basic problem with photons is the one identified by the Mother Superior in The Sound of Music: how do you catch a wave and pin it down? Atoms, however, are another matter. You can catch an atom in a trap by using electric or magnetic fields to confine it. And that’s what the two teams of researchers did to accomplish atom teleportation. Rainer Blatt and colleagues at Innsbruck held three calcium ions in an electromagnetic trap; the NIST team in Boulder used the same kind of trap, but their quantum particles were beryllium ions. Both groups used lasers to place the ions in excited electronic states: the aim was to transfer the complete quantum state of one ion to another ion.

The researchers needed to be able to address each of the ions individually with the laser beams. They used different strategies for that. Blatt’s group captured the ions in a regularly spaced row, 5 ?m apart, and then interrogated some of them without disturbing the others. They ’read out’ the ions’ electronic states by inducing fluorescence with a laser. But this emitted light could potentially interfere with the whole process. ’If we want to keep the quantum information on the third [target] ion in the teleportation process, we want to protect this information from being affected by stray light’, Blatt explains. They did this by ’hiding’ the target ion: putting it into an electronic state that cannot absorb the light involved in the measurement process on the other ions. The ion trap of Wineland’s group, meanwhile, was divided up into six different trapping zones. Using electric fields, the researchers could move each ion individually between zones during the teleportation process to keep them isolated when necessary.

One key step is placing the ’messenger’ and ’target’ ions in an entangled state. ’Entanglement requires that the internal states of the two ions are intricately interwoven’, says Blatt. Both groups use an optical signal as a kind of ’entanglement force’ which excites the ions’ motions in a way that binds them together. ’The ions feel each other once they move, because the Coulomb [electrical] repulsion between ions pushes them back’, Blatt explains. ’We use this motion to let ions "know" of each other in a correlated way.’

Both groups were able to achieve teleportation of an ion on demand, but not perfectly. That’s to say, the target ion wasn’t a perfect copy of the original; rather, only about 75 per cent of the original quantum state was reproduced in the target. That, however, is still better than what can be achieved classically by making measurements on one ion and then using that information to prepare a ’replica’. The classical copying fidelity can be no greater than two-thirds. The extra fidelity in the quantum case was due to the information sent from one ion to another down the entanglement link. Both groups think that it should be possible to boost the fidelity of their schemes. ’Most of the errors are "classical", for example caused by fluctuations in laser intensity’, Wineland says. ’There are straightforward ways to improve these errors. Now we actually have to do it.’ Blatt thinks that ultimately a fidelity of at least 99.9 per cent should be possible.

Entangled computing

Achieving this ’deterministic’ teleportation, which can be reliably conducted at the push of a button, changes the game completely. It is a ’landmark advance’, according to quantum physicists Jeff Kimble at the California Institute of Technology, US, and Steven van Enk of Bell Labs in New Jersey, US. In particular, controlled teleportation could be used to ’wire up’ quantum computers, which would have orders of magnitude more computing power than today’s conventional computers.

In a quantum computer, information is encoded not in traditional ’bits’, which can be in one of two states (say, 1 or 0), but in quantum bits or qubits. These can be placed collectively in superpositions of quantum states: not only 1 or 0, but also combinations of the two. That vastly increases the number of states a quantum computer can access, boosting its power enormously. In effect, the superpositions allow a collection of qubits to act as many computers at the same time, enabling the device to perform many calculations in parallel. Quantum computers could solve difficult problems, such as factorising numbers, in a fraction of the time it would take a conventional computer to do the same task.

The trick, however, is to master the delicate balancing act of keeping large numbers of qubits in quantum superpositions, without them ’collapsing’ into one state or the other. This happens through a phenomenon called decoherence, which is basically caused by interactions between the qubits and their environment. The challenge in making a quantum computer is to isolate the qubits sufficiently to suppress decoherence while still enabling information to be read in and out. At present, no one has managed to achieve a quantum computational operation with more than three or four qubits.

Ions held in ion traps are considered one of the most promising systems for providing a quantum computer’s qubits. ’Atomic qubits are able to store quantum superpositions much longer than can be done with photons, so they make good memory elements in a quantum processor’, Wineland says. His group has been able to preserve particular superposition states in ions for more than ten minutes. Quantum entanglement could provide a way of wiring up remote qubits in such a scheme: it would be a form of ghostly ’quantum wiring’. And quantum teleportation along these quantum wires would enable information to be shifted around the computer with perfect accuracy.

Wineland also foresees the use of atoms as memory elements in a quantum communication network. Here, information would probably be passed around using photons, just as it is in today’s telecommunications. The photonic quantum states would then be mapped onto atoms at a receiving station. Blatt says that there could also be applications in high-precision measurements, where entanglement provides a very sensitive probe of the environment. And because entanglement operates over arbitrary distances, it could be used to develop new kinds of sensor. His laboratory is now exploring these possibilities.

Could teleportation really be used to shift chemical matter around - might it work for a molecule or a group of atoms? Complete molecular quantum teleportation would produce a copy that is in exactly the same translational, rotational, vibrational and electronic state as the original - in other words, there are a lot of degrees of freedom to get right. ’Teleporting states of groups of atoms or molecules requires more horsepower than we currently have’, Wineland admits, ’but if we can continue to improve our experiments, it should be possible.’

Blatt agrees that a teleported molecule is feasible in principle, but the technical challenges would be daunting. ’The basic scheme would be the same’, he says, ’but retrieving the original rotational-vibrational state would require an enormous overhead. At this time nobody really knows how to handle that.’ For the time being, it seems we’ll still have to rely on the mail.