A golden answer to drug competition

The golden ratio, first noted around 300BC by Euclid in his mathematical treatise The Elements, can be found across geometry, nature and now even pharmacology. New research has shown that the golden ratio could point the way for a simple method of determining competition between drugs.¹

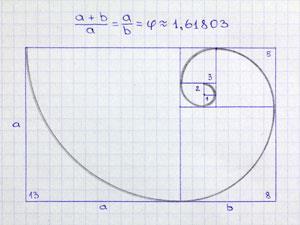
Known as f, the golden ratio of 1.618 defines the ratio between two numbers such that their sum is the same ratio to the larger of the two. While this may at first appear to be only a mathematical curio it defines the most aesthetically-pleasing rectangle, the ratio between bones in the finger and even a series of frequencies in solid-state magnetic resonance.²

Gavin Jarvis and Andy Thompson, from the University of Cambridge, UK, made their discovery when they were looking for a simple technique to determine whether two drugs bind to the same site (syntopically) or can bind to different sites (allotopically). This is an important question as drugs are commonly used in combination to prevent resistance, improve outcomes or reduce side-effects.

Using ion channel blocking drugs as a model, they compared the theoretical effects of two drugs in syntopic and allotopic scenarios. By using differentiation to find the maximum difference between the two models, the authors found that the optimum concentration of the drugs is the level at which half the ion channels are inhibited times f. This is the point where they would cause 61.8% (1/f) inhibition when acting alone.

'The answer we got was counter-intuitive, but our maths was supported by our experimental data,' Thompson says. 'The golden ratio has intrigued mathematicians, scientists, artists and philosophers for millennia ... until now, no role for the golden ratio has been identified in pharmacology, or phi-macology as we termed it.'

Under these optimum conditions the allotopic model would result in 85% inhibition, while the syntopic model would yield only 76%. With this relatively small difference between the two scenarios, statistical analysis is still necessary before drawing conclusions.

The authors chose channel-blocking drugs to study because they behave 'much as a cork stoppers a bottle' with zero occupancy having no effect and full occupancy resulting in full inhibition. Although the theory works well for the chosen experimental model using bilobalide, ginkgolide and diltiazem to inhibit the 5-HT₃ receptor, complications can arise in other systems where the drugs may interact and binding is not independent.

Matteo Goldoni, from the University of Parma, Italy, comments: 'The approach of the authors is interesting although it is applied to a simple case. In particular their suggestion to use the golden ratio and the statistical suggestions [are] original and quite promising.'