Nyquist’s frequency

It drives me crazy when people refer to the ‘arts’ as being creative. Is the implication that science and technology is a desert of enforced intellectual servitude? Someone who lived in a hive of technical creativity was Harry Nyquist, one of the founders of information theory, whose ideas underpin most of the tech we use today.

Nyquist was born in a small village in Sweden in 1889, one of seven siblings. Along with many other Scandinavians, his family emigrated to the fertile plains of the middle west of the US, a cultural milieu made famous by Garrison Keillor’s Lake Wobegon Days and the Cohen brothers’ film Fargo: stoic communities of farmers who sought comfort through hard work and quiet religious observance.

Nyquist rapidly established himself as top of his class at high school. At first he dreamed of becoming a teacher. But by the time he graduated, he had been bitten by the physics bug. He moved west to the nearby University of North Dakota, where he befriended John Bertram Johnson, another young physicist. The pair then headed to Yale, Nyquist focusing on atomic physics.

After graduating with his doctorate in 1917, both he and Johnson got jobs at the AT&T research labs in New York City, the precursor to the legendary Bell Labs. Here, Nyquist was in his element. He was surrounded by some of the smartest people in science and technology, in an environment that placed no boundaries between disciplines. Theoreticians talked to experimentalists, engineers to chemists and physicists. Industry was growing at breakneck speed – steel production, for example increased five-fold between 1900 and 1920, and cables for both electrical transmission were criss-crossing the country. Radio stations were springing up in every small town.

There was a real sense that scientific and technical creativity were fundamental to achieving national prosperity. Employees of the great commercial research labs – General Electric’s in Schenectady, DuPont’s in Wilmington, for example – had freedom to explore fundamental questions. Many companies including Bell, Phillips and Siemens even published their own scientific journals to present their discoveries.

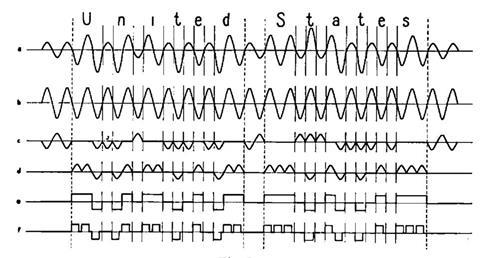
Nyquist began to explore the mathematical basis for signal transmission, methodically exploring different possibilities for the shapes of the carrier signals, optimal frequency ranges and the use of single or dual transmission of signals. He began to develop a mathematical theory of signalling that included an expression remarkably similar to Claude Shannon’s later expression for informational entropy. One of Nyquist’s key conclusions was the link between the fundamental frequency at which data was carried and the data that was encoded on top of it. Any data required the carrier to have a frequency at least twice that of the data itself, to ensure that it was uniquely encoded.

Turned upside down, his principle, later extended by Shannon, would become the cornerstone of digital instruments. Any varying signal must be sampled at a rate at least twice that of the variation in the signal itself to be recorded without distortion. Any frequency components higher than this Nyquist–Shannon limit are ‘aliased’ and hence recorded in the wrong place. The example most familiar to chemists comes in Fourier Transform NMR spectroscopy: the width of the spectral window is determined by the frequency at which the signal is sampled by the spectrometer. Peaks outside the spectral window ‘fold back’ into the spectrum in odd places and with peculiar phases.

Nyquist worked quietly but intensely, writing his equations in pencil on those classic American pads of yellow paper that I remember from my childhood. He was extraordinarily regular in his habits. His daughter would later remember that his alarm would ring at 6.45 each morning. Nyquist would get dressed while his wife prepared breakfast, and be out the door at 7.30 precisely, to catch the train into the city. He would return punctually at 6.15pm in time for dinner: ‘You could set your watch by it’. At weekends he did domestic chores and went to church, often returning to his yellow pads to push his thinking a little further.

His mathematical ability was widely admired. In the late 1920s his friend Johnson began wondering about the origins of noise in electrical circuits, developing methods to measure it precisely but failing to explain it. Nyquist set to work and in a few weeks had developed a complete description of the problem by combining electrical theory with statistical mechanics, showing that its power was proportional to temperature and the resistance of the circuit. Today, thermal noise is also known as Johnson-Nyquist noise.

Nyquist’s final major contribution came from thinking deeply about the problem of feedback in resonant circuits, trying to understand under what conditions a circuit would become unstable. In radio terms that meant a whistle or howl, for a motor possible burnout. Nyquist developed a general theory that included an elegant graphical representation of the frequency response of the system. Long before computational simulation, one could predict in advance how an electrical motor, a radio circuit or an electrical generator would behave. Today, the Nyquist plot is one of the key tools used by electrochemists to investigate the kinetic processes taking place inside batteries, because it gives representation of the charging and discharging characteristics of the cell across a wide range of frequencies.

Nyquist continued to work at Bell Labs until 1954. An attempt to understand why certain employees were responsible for more patents than others uncovered the curious observation that the more creative often had breakfast with Nyquist. As a colleague recalled ‘he drew people out, got them thinking’. We all need people like Nyquist down the hall.

Acknowledgments

I’m very indebted to my friend Christoph Salzmann for reminding me of the Nyquist frequency in a lecture on instrumentation.