A new deep-learning algorithm from researchers in Austria has produced more accurate numerical solutions to the Schrödinger equation than ever before for a number of different molecules at relatively modest computational cost – although the work itself may subsequently have been surpassed by research from Google’s DeepMind. Surprisingly, the Austrian researchers found that, whereas some ‘pre-training’ of their algorithm could improve its predictive abilities, more substantial training was actively harmful.
As the Schrödinger equation can be solved analytically only for the hydrogen atom, researchers wishing to estimate energies of molecules are forced to rely on numerical methods. Simpler approximations such as density functional theory and the Hartree-Fock method, which is almost as old as the Schrödinger equation itself, can treat far-larger systems but often gives inaccurate results. Newer techniques such as complete active space self-consistent field (CASSCF) give results closer to experiments, but require much more computation.
To find more accurate solutions to the wavefunctions of molecules more expeditiously, researchers have developed deep-learning algorithms that sample the energies at multiple points and teach themselves to search for the molecule’s ground state. ‘Often people have been running an established numerical scheme and then using a machine-learning algorithm to try to learn the details that are missing,’ explains Philipp Grohs of the University of Vienna.
Grohs and colleagues at the University of Vienna began from the two leading machine learning algorithms in the world: FermiNet – developed by Google’s DeepMind – and PauliNet – produced by researchers in Berlin. FermiNet has a simpler, more efficient structure and tends to reach more accurate solutions, whereas PauliNet feeds in more details from established schemes about what the solution should approximately look like and therefore tends to work more quickly.
Grohs and colleagues at the University of Vienna developed an algorithm using the simple structure of Ferminet, but incorporated an element of PauliNet called SchNet originally designed for calculating the configurations of atoms in molecules. ‘We tried to better model the particle interactions by using the ideas from SchNet,’ explains Leon Gerard. The final algorithm achieved greater accuracy, and required fewer computational resources, than either FermiNet or PauliNet for a variety of molecules ranging from nitrogen and water to benzene and glycine. The accuracy of the algorithm, which is detailed in a paper to be published in the journal NeurIPS, may itself now have been surpassed in another neural network algorithm pre-print from the DeepMind group released in November. David Pfau from DeepMind describes the new algorithm as ‘far more accurate than the work of the group in Vienna’ although the Austrian researchers respond that the DeepMind researchers have not yet published their code and that therefore ‘a like-for-like comparison is currently hard to make’.
The researchers tested the effect of ‘pre-training’ steps, in which they used either Hartree-Fock or CASSCF to teach the algorithm to find an ‘appropriate’ starting point in its searches for the ground state. Unexpectedly, they found that, whereas a modest number of pre-training steps improved the performance, too much pre-training caused the algorithm to miss the actual ground state. Moreover, this was more pronounced when they trained the algorithm using CASSCF than when they used Hartree-Fock. The reasons are unclear. ‘CASSCF imposes much more structure on the wavefunction – so there may be many more nodes and a much more complicated shape, so if the neural network learns something that’s complicated and wrong, it may learn something that’s harder to escape from – but I don’t think we really know at this point,’ explains author Michael Scherbela.
Isaac Tamblyn of the computational laboratory for energy and nanoscience at the University of Ottawa in Canada, who was not involved in the work, describes it as among the most impressive results to date, although he does not find the counter-intuitive effects of introducing prior knowledge especially surprising. ‘There are lots of examples in the optimisation literature where you can try to incorporate what you think is a helpful initialisation that ends up making the situation worse,’ he says. He describes the work as excellent but points out that, while it may be more efficient than methods like FermiNet, it still takes several days on a GPU to compute the properties of a single molecule. He suggests that its principal use, therefore, is likely to lie in producing highly accurate training data for approximate methods such as supervised machine learning.
This story was updated on 12 January 2023 to provide more context on the accuracy of the Austrian group’s solutions of the Schrödinger equation and how it compared with other efforts.
References
L Gerard et al, arXiv, DOI: 10.48550/arXiv.2205.09438

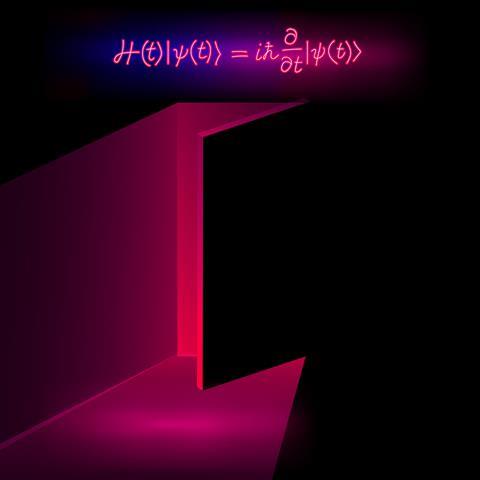













No comments yet