Algorithm out of Google’s DeepMind finesses DFT calculations

A neural network constructed by researchers at Google’s artificial intelligence arm DeepMind has produced a refined density functional theory algorithm. The algorithm, which considers ‘fractional electronic character’ overlooked in previous DFT algorithms, is able to avoid some of the pitfalls that often lead these algorithms to give highly inaccurate results.

The Schrödinger equation cannot be solved analytically for any atomic system more complex than the hydrogen atom because electron–electron repulsion means the variables involved increase dramatically. This means that to create realistic approximations of molecular systems, researchers have to turn to computational methods. For some small molecules, it is feasible to find approximate numerical solutions to the equation for each electron and estimate the shape of each molecular orbital from the resulting wavefunctions. However, the computational demands are huge and grow steeply, as every additional electron repels every other. ‘The question is how do you go beyond this area?’ says DeepMind’s Aron Cohen.

In the 1960s, Pierre Hohenberg and Walter Kohn showed that, in principle, one could map a molecule’s electron density precisely to its energy. As a molecule would tend to adopt its lowest energy state, chemists could theoretically predict the state of a molecule without knowing the state of any single electron. Kohn later shared the 1998 Nobel prize in chemistry for his work, which gave birth to DFT. The work does not, however, reveal how to compute the electron density, and researchers have worked to find better ‘density functionals’ to do this ever since.

Theoretical chemists have worked out an ever-growing list of constraints that accurate density functionals should satisfy. Two of these, which concern the delocalisation of electronic spin and charge between atoms in a molecule, are highly problematic. ‘For example, if you have H₂⁺ in this system on average you will have half of the electron on one hydrogen and half of the electron on the other side,’ explains Cohen’s colleague James Kirkpatrick. ‘Most functionals predict that, even at infinite distance, those two atoms are bonded – this is a large error in DFT caused by the fact that functionals get confused by the fact that it’s just one half of a whole electron.’

The researchers created a self-learning neural network and trained it on fictitious systems. ‘If one thinks of an atom, one can also think of the electron density if one removes an electron or half an electron,’ explains Cohen. Through a process of feedback and self-correction, the neural network learned to predict the electron density around small molecules.

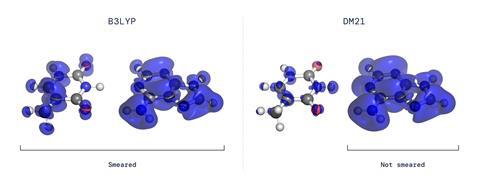
The researchers then put the functional, which they named DM21, to work on several problems of interest. For example, they looked at charge transport in DNA by predicting the charge density distribution in the ionised adenine–thymine base pair: whereas a popular functional today suggests the charge is distributed across the two bases, their functional correctly predicts it to be concentrated on the adenine alone. They also looked at the simpler example of bicyclobutane, for which more fundamental computations do exist, and showed that the results from their functional were similar. The researchers are making DM21 freely available to all chemists on GitHub. They now intend to train it to study more complex bulk interactions in transition metals, for example, and hope it may provide insights into phenomena such as cuprate superconductivity.

‘There’s nothing new in applying machine learning to construct density functional approximations,’ says John Perdew of Temple University in the US, noting that the idea was first proposed in the 1990s and has been used in ‘many papers in recent years’.

‘The novelty in this work is that they satisfied recalcitrant but important mathematical constraints by turning them into data that a machine can learn from.’ He notes, however, that the use of the fractional spin constraint to find the energy of the ground state ‘comes at a cost’, as small energy differences between the ground and excited states can lead to spin oscillations and spin symmetry breaking, which are crucial to the properties of materials such as antiferromagnets – as well as the cuprate superconductors.