The simple machine that visualised atomic orbitals

The invention of quantum mechanics – a mathematical method for calculating quantum states of atoms – 100 years ago by Werner Heisenberg was followed soon after by Erwin Schrödinger’s rival scheme, commonly known as wave mechanics. While Heisenberg tabulated the frequencies of spectral transitions in matrices, Schrödinger – who published his famous equation in early 1926 – represented the behaviour of quantum particles such as electrons in a form that looked reassuringly like a conventional equation of motion.

Instead of a trajectory, there was a wave function, which Schrödinger initially thought represented the electron density at each point in space. But later in 1926 the German physicist Max Born proposed that the wave function in fact defines a probability distribution: the amplitude of the wave function at a given point is proportional to the chance of finding the electron at that position if it is measured.

Applying Schrödinger’s equation

It is in this ‘Born rule’ that the fundamental peculiarity of quantum mechanics resides, for it tells us that the basic equation speaks not to the nature of the particle but to the outcome of a measurement of it. But while the implications of that idea continue to be argued over today, at the time the first quantum physicists were delighted with Schrödinger’s equation because it was so much easier to calculate with than were Heisenberg’s ungainly matrices. In Zürich, where Schrödinger was based, his postgraduate student Walter Heitler worked with Fritz London to apply the equation to the hydrogen molecule, extending the new quantum mechanics from atoms to molecules and thereby developing a quantum theory of the chemical bond.

Later in 1926 Schrödinger was visited by American chemist Linus Pauling, who was on a Guggenheim Fellowship to study in Europe. Encountering the work of Heitler and London, Pauling decided to devote himself to formulating a quantum theory of the structure of molecules. In the late 1920s he began publishing pioneering papers on the chemical bond, culminating in his groundbreaking 1939 book The Nature of the Chemical Bond, the standard text on quantum chemistry for decades after.

But for all this, it was tough for researchers to solve the Schrödinger equation exactly for systems with more than one electron. Heisenberg and Born had insisted in the mid-1920s that one had to relinquish the old picture of electrons in atoms being confined to orbits; instead, the Schrödinger equation now presented the picture of smeared-out clouds of probability density, which differed for the different quantum numbers that characterised electron states in atoms. Pauling and others figured out that these probability distributions typically consisted of several lobes – what we now recognise as the familiar dumbbell-like p orbitals and so forth.

From mechanics to mechanical

Today these electron probability distributions can be computed numerically. But before the development of programmable computers it was far from straightforward to deduce their three-dimensional shapes. In 1931, however, a physicist named Harvey Elliott White at the University of California at Berkeley described an ingenious analogue simulation.¹ He invented a mechanical device that, when set in motion, followed a trajectory that approximately traced out the electron clouds of the various orbitals in atoms.

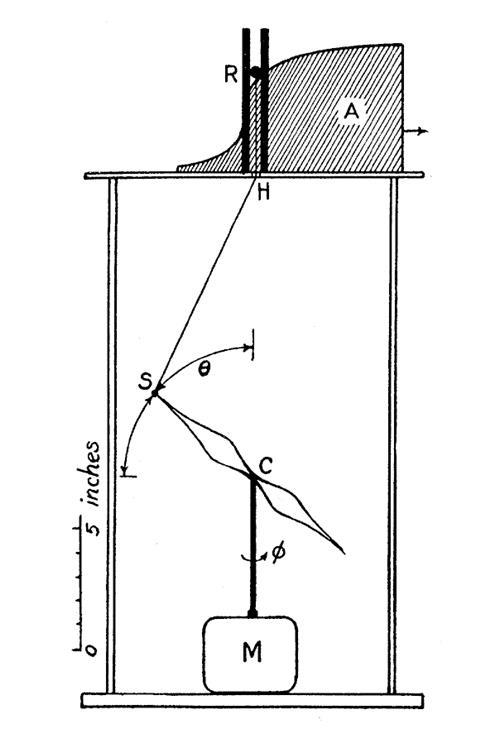
It was a fairly simple machine. A motor, enclosed in a box, drove a vertical spindle to the top of which a propellor-like arm was attached, which was free to tilt from horizontal to vertical as well as to rotate. These movements essentially replicated the solutions to the Schrödinger equation in polar coordinates, with differently shaped propellors corresponding to different quantum numbers. A long-exposure photo of the motion inside the dimly lit box provided an image that more-or-less represented a two-dimensional projection of the corresponding electron clouds, complete with fuzziness at the edges of the orbitals. In this way White could reveal not just the familiar spherical and concentric clouds of s orbitals and the twin lobes of p orbitals but also the complicated and hard-to-calculate shapes of, say, 5f orbitals.

It was a clever use of the analogy between the Schrödinger equation and the equations of classical wave mechanics. To develop the idea, White consulted with Robert Oppenheimer, who had himself studied under Born and developed the Born–Oppenheimer approximation (assuming electrons move much faster than nuclei) for calculating molecular wave functions.

White stayed at the Berkeley physics department for his entire academic career (aside from a short spell at Pittsburgh), working briefly with Ernest Lawrence. He later became a prominent science communicator, being the founding director of the Lawrence Hall of Science, a public science centre, in 1959 and presenting educational programmes about physics on TV. His mechanical quantum-simulation device perhaps sowed the seed for White’s later innovation at Berkeley – a lecture theatre (Pimental Hall) for physics and chemistry with a rotating stage that allows several lecturers to teach, clean up and set up at the same time.