Instanton theory extended to describe quantum tunnelling through a conical intersection

Theoreticians have developed a new method for calculating molecular transition rates on non-trivial energy landscapes. Their slimline approach not only reduces intractable many-body mechanics to manageable computations, but also lets them quantify the individual phenomena that assist or hinder transitions.¹

Many-body quantum mechanics forms the mathematical basis for understanding molecular behaviour. But while it is one thing to write down the equations that describe how a system’s many electrons and nuclei interact, solving them exactly is quite another. Theoreticians must therefore use tricks to simplify their calculations, the most famous being the Born–Oppenheimer approximation. Taking advantage of the fact that electrons are much lighter than nuclei, the electron wavefunctions can be computed first, which then form a potential energy surface, or landscape, on which the nuclear wavefunctions are solved.

However, Born–Oppenheimer ceases to be valid when the energy landscape of one state stumbles into another. The point where the ground state and an excited state of a system form cone shapes that touch each other tip-to-tip is known as a conical intersection. Conical intersections are important in many photoexcited reactions – for example, DNA repairs itself after UV irradiation by dropping through such a cone.

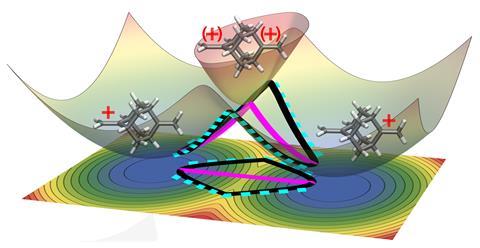
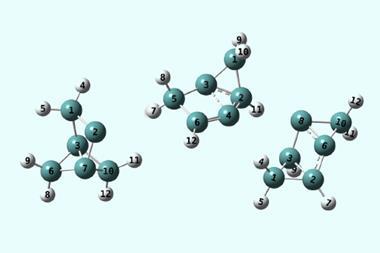
Another scenario is the thermally activated transition from one local minimum of a ground state to another. The excess positive charge of a bis(methylene)-adamantyl cation periodically shifts itself from one side of the molecule to another, but to do so it must pass through a conical intersection. This is a simple model system for studying the principles at play, but already it poses a formidable computational challenge.

‘The standard approach would be to use the Schrödinger equation for the nuclear wave function, and for a three- or four-atom system, you’d have no problem in doing that,’ says Jeremy Richardson, of ETH Zurich, Switzerland. But for a molecule with 20 or so atoms? ‘Absolutely no chance of doing this on modern computers, nor even in the foreseeable future.’

So, Richardson and colleagues at ETH Zurich and Fudan University in China devised a scheme to capture the essential quantum effects while avoiding intensive calculation of less important aspects. Instead of the Schrödinger equation, they turned to the path-integral formulation of quantum mechanics, which accounts for every possible route the system might take to get from A to B. But this too would be unviable, so the researchers simplified things further by homing in on the most likely routes – a technique called instanton theory.

Quantum route-planning

‘This is a bit like when you ask Google to tell you what the best route is to travel from Oxford to Cambridge or whatever, and it will give you the most efficient route out of the infinite number of routes,’ says Richardson. ‘You guess one, and then you make small modifications to it, and you keep making small modifications to it, until it gives you the optimal path. It’s the computer’s version of trial and error.’

As well as being efficient, this quantum route-planning allows the researchers to pinpoint individual factors that make the journey easier or harder. For example, the system can avoid an arduous climb up the cone by instead tunnelling through it. Quantum tunnelling is a well-known phenomenon, but Richardson was surprised at just how readily it occurred.

‘People are used to this concept for hydrogen atoms, because they are lighter and therefore much better at tunnelling through the barrier,’ he says. ‘For carbon atoms tunnelling, it’s effectively assumed that this will never happen at room temperature, but we find that it does.’ He argues that the narrow, pointy shape of a conical intersection makes tunnelling more amenable than has hitherto been appreciated.

Another key effect – this time one that hampers the transition – is that of the geometric phase. Artur Izmaylov, a theoretical chemist at the University of Toronto, Canada, who has studied this effect in the same system but by a different method,² explains that routes winding around the cone on its righthand side cancel out those that wind around its left, because of a quantum phase difference arising between the two.

‘The important contribution [of Richardson’s team’s work] is that they account for not only tunnelling, which instantons would do, but also the destructive interference,’ Izmaylov says. ‘That’s very appealing from the point of view that if we would like to think about quantum phenomena classically, this is a relatively simple picture to have.’

Interestingly – and disappointingly, as Richardson admits – for the simple case of bis(methylene)-adamantyl, the speed-up from tunnelling is more or less undone by the geometric slow-down, but he says this is a coincidence that will not hold generally.

‘Conical intersections are ubiquitous, and we are going to be looking to find examples where tunnelling and geometric phase effects are important for biologically relevant systems,’ Richardson adds. ‘I am sure that we will find some and it will tell us that the human body only really works because of all these weird effects. I’m very excited to find specific examples of that, and then to get experimental backing for proving it to be true.’