Electric fields bring new dimension to debate on atomic size

No comments

How big is an atom? On the order of ångströms, scientists agree, but putting a precise figure on a given element is trickier. For ions and molecules, even more so.

Answers have been offered from a variety of empirical sources, with everything from compressibility and crystal structure to optical refraction and electrical polarity being used to quantify what is known as the Van der Waals radius – named after the scientist who theorised finite molecular size in gases. Researchers have also turned to quantum mechanics and computation, calculating electron wavefunctions – the clouds of probability that surround atoms – and using a sensible cut-off value to mark out an atomic boundary.

A team at the University of Oregon, US, has now proposed a new metric: the electric field that surrounds every atom. Led by Christopher Hendon, they have developed a software package to calculate this electric field, which arises under the net influence of the atom’s nucleus and electrons, and quantify its extent in space.

For neutral, non-interacting atoms, the charge of the electrons balances the nucleus, cancelling out the electric field beyond. Indeed, using their field-based method, the team’s calculations were in line with established values. ‘We match closely to the accepted Van der Waals radii,’ says Hendon. ‘That’s a good sanity check.’

Source: © Christopher Hendon/University of Oregon

Conventional chemical tenets suggested by Batsanov would indicate that Mg²⁺, and cations in general, are smaller than their neutral counterparts. Yet, from an electrical field perspective, Mg²⁺ should be significantly larger than Mg⁰, because the electric field ultimately depends on the ratio of the number of protons-to-electrons

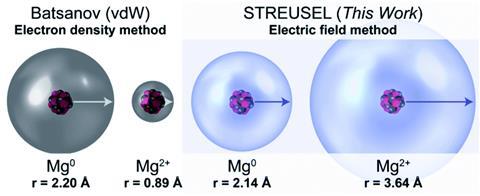
Ions are where, in Hendon’s words, the model ‘really takes a turn for the interesting’, as illustrated for the case of Mg²⁺. Under the conventional measure of electron density, this cation is more compact than its neutral counterpart, due to lacking its outer electrons. The electric field picture, however, shows a size increase. This is because the nuclear charge is no longer fully screened by the electrons, so the field can pervade further into space.

The advantage of this approach, Hendon argues, is that it corresponds to the region that the ion affects, which could be more relevant than the region it occupies, especially when choosing materials for applications. The result for Mg²⁺, he suggests, might explain why magnesium-ion batteries do not perform well. ‘The magnesium sticks to everything… It doesn’t move that easily, unlike other ions.’

For anions too, the model draws surprising conclusions, not least when comparing elements. Under the field-based model, a Br^- ion turns out to be larger than I^-, and F^- is bigger still. This reversal comes about because the extra electron on a bromide ion has its field reined in by the larger nucleus. ‘You’re basically diluting the negative charge by more positive species,’ Hendon explains.

Santiago Alvarez, an electronic structure expert at the University of Barcelona, Spain, cautions against too literal an interpretation. ‘To compare with a macroscopic situation, would we define the size of a magnet as the extent of some cut-off of its magnetic field?’ he asks.

Alvarez, who has also worked on quantifying atomic size, points out that the electric field is only one means by which nearby atoms can interact, with Pauling repulsion, orbital dispersion and spin–spin interactions being others. And he highlights complications that may arise when atoms form bonds: ‘How could we apply the radius of Fe³⁺ [calculated by Hendon’s team as approximately 4.2Å], to species such as the FeO₄^5- anion, in which the oxygen atoms are barely 1.90Å from the iron nucleus?’

Hendon is keen to stress that his approach should complement, not replace, the existing ones. ‘The Van der Waals radii are backed up by experimental data. This has been extremely valuable.’