Pressure used to define relationship between atomic radii and electronegativity

Researchers in Sweden and Italy have derived an equation that illustrates how van der Waals radii and electronegativity relate to each other as a function of pressure.¹ ‘This connection has been implied for a very long time; it’s very intuitive in a way. If electrons are closer to a nucleus they are more bound and the atom is both smaller and more electronegative,’ says Martin Rahm of Chalmers University of Technology, Sweden, who led the study.

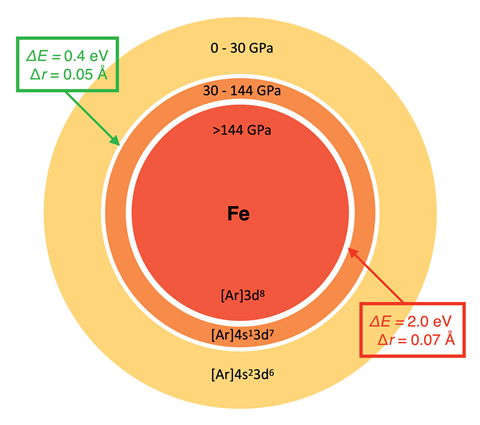
In previous work,^2,3 Rahm and his colleagues used density functional theory combined with the extreme pressure polarisable continuum model to calculate van der Waals radii and electronegativity for 93 atoms at pressures from 0 to 300GPa. They recently compiled these data, along with spins and ground state electronic configurations, into an app. Pressure is known to induce transitions of the ground state electronic configuration of many atoms, and their Atoms-under-pressure app highlights the sharp discontinuities predicted in atomic radii and electronegativity at such transitions. Through exploring the criteria for non-bonded atoms transitioning at a given pressure between competing electronic states, Rahm’s team has now derived an equation relating atomic radius and electronegativity. They say this expression can, for example, help rationalise how reducing an atom’s oxidation state under ambient conditions decreases its electronegativity, and vice versa upon oxidation.

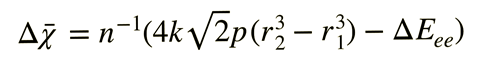
Other scientists have reported frameworks that relate electronegativity to atomic radii under pressure, but Rahm says that these are often only applied to a few atoms – not systematically across the periodic table, and usually don’t provide given pressures. ‘We’ve paid a lot of attention to having a model that corresponds to something measureable, and we give these properties at a given pressure,’ he explains. Rahm envisages researchers might use his team’s dataset in areas such as high-pressure structure prediction (eg to derive a good starting approximation for the unit cell volume), for defining molecularity in compressed systems, identifying bonded atoms and for property prediction. Though he acknowledges it may be harder to use atomic properties under compression: ‘The degree to which bonding messes with your rationales is what’s going to determine how useful they are.’

‘It is an important contribution,’ says computational chemist Pratim Kumar Chattaraj from the Indian Institute of Technology Kharagpur. However, Chattaraj cautions that ‘structure, bonding and reactivity undergo a drastic change in a confined condition. Variation in all the atomic or molecular properties may not follow the same trend and hence the related correlations valid in the free state may not be true in a confined situation.’