Magic numbers for jellium aromaticity could help researchers find stable high-spin molecules
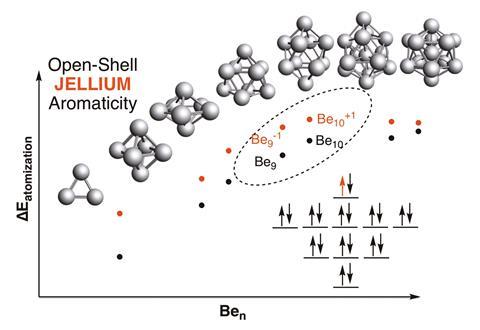
Aromaticity is evident in metal clusters when studied using the jellium model of electrons in a solid, new research shows. By extending the rules that govern aromatic character in planar and spherical molecules, scientists in Spain have put forward analogous rules for open-shell jellium clusters.1
Ever since Hückel’s (4n + 2) rule for denoting planar ring molecules with delocalised π-type molecular orbitals, chemists have sought other electron counting methods to help them foresee and explain stable chemical species using aromaticity. These methods include Hirsch’s 2(n + 1)2 rule for predicting spherical aromatic species. Like Hückel, Hirsch’s rule requires filled outermost orbital shells. Then there’s Baird’s 4n π-electron rule to explain aromatic behaviour in planar ring molecules when their outermost molecular orbitals are only half-filled with electrons.
A previous study, on applying the jellium model (see box), found that metal clusters with ‘magic numbers’ of valence electrons – that also result in a full outer electronic shell – display aromatic stability.2 Here, aromaticity refers to delocalised electrons across the body of the cluster, rather than over a planar ring or spherical surface.
Back in 2011, Miquel Solà from the University of Girona and Jordi Poater from the University of Barcelona extended Hirsch’s formula to open-shell spherical compounds.3 Now, Solà and Poater have proposed equivalent scenarios that apply to open-shell jellium clusters. By considering small to medium sized clusters of sodium and beryllium, they have shown that clusters with a half-filled highest-occupied jellium energy level are more stable than those that do not. This aromatic character results in higher atomisation energies; an indicator of stability.
It would be nice to have a unified theory – but I think we are quite far away from that goal
By extending established rules governing open-shell aromaticity, Solà and Poater were able to suggest a new series of magic numbers, which could help researchers to synthesise stable, ground state clusters in high spin configurations.
‘When you have open-shell situations, you have high spin molecules, and these high spin molecules are interesting for single molecule magnets,’ explains Solà. Single molecule magnets retain magnetic information up to a certain temperature so are candidate materials for high-density magnetic data storage, sensors and quantum computing.
‘This is definitely a fine contribution to cluster science, and indeed prompts the question why this extension of the jellium model hasn’t been found or reported before, as it appears to be so intuitive,’ comments Stefanie Dehnen, a cluster chemist at the Philipps University of Marburg, Germany.
‘Yet, I am struggling with the term aromaticity in the context of metal cluster chemistry,’ Dehnen adds. ‘In my view, the term superatom is much more appropriate and perfectly meets the outcome of the study.’
Solà hopes the extended rules will inform future investigations into the nature of aromaticity: ‘It would be nice to have a unified theory, looking at connections between different rules of aromaticity that affect different situations and trying to connect them, or trying to see if there is some relationship between them.’
However, he admits it is still too early to be talking about a complete theory of aromaticity. ‘Maybe – maybe – it would be possible to have a kind of unified theory. But I think that at the moment we are quite far away from that goal.’
Jellium model
At face value, the similarity between molecules and clusters is not obvious. Understanding the electronic structure of clusters, however, is achievable using the jellium model. This is a quantum mechanical model that treats the positive atomic cores of a cluster as a uniform distribution of positive charge across space and the valence electrons as homogenous and delocalised electron density. The equations on which this relatively simple model is based can be solved computationally using fewer resources than alternatives, and provide accurate results for clusters that have symmetrical, near-spherical geometries.
The electronic energy levels that result from the jellium model have explained the abundances of various clusters, with the most common clusters in experimental studies corresponding to the closed-shell, stable clusters predicted by the jellium model.
References
1 J Poater and M Solà, Chem. Commun., 2019, DOI: 10.1039/c9cc02067e
2 T Höltzl et al, Aromaticity and Metal Clusters, 271–296, Boca Raton: CRC Press, 2010
3 J Poater and M Solà, Chem. Commun., 2011, 47, 11647 (DOI: 10.1039/c1cc14958j)







No comments yet