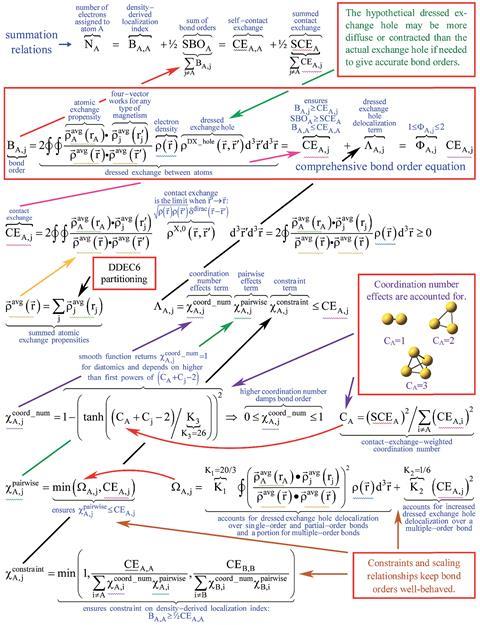
Comprehensive equation derives bond orders from quantum chemistry calculations
A researcher in the US has proposed a new way of computing bond order, which he says is more general and more consistently accurate across diverse kinds of materials.
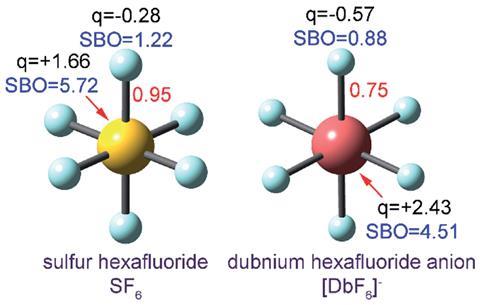
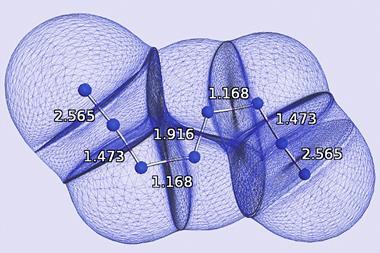
Bond order quantifies how many electrons two atoms in a material share. But it’s a theoretical concept, not something you observe experimentally, so defining it and calculating it can get a bit fuzzy. ‘Some new chemistry students find it difficult to memorise which rules apply to which chemicals. For example, why should N2 and CF4 be described by a Lewis structure while triplet O2 and SF6 are not?’ says Thomas Manz of New Mexico State University. ‘My method introduces a unifying principle where you no longer have to memorise different rules for different materials. All you have to do is calculate and you will get the accurate bond order,’ he explains.
Previous methods for calculating bond order have failed to give consistent results. ‘The method that Manz has introduced overcomes a variety of deficiencies of other bond order schemes,’ comments Roger DeKock, emeritus professor of computational chemistry at Calvin College, Michigan, in the US. ‘For example, many methods do not show a steady decrease in the bond order of H2 as the bond is stretched. The method of Manz, fixes this problem and many others. It does so elegantly, but at the cost of introducing three empirical parameters,’ he adds.
To use Manz’s method the user must obtain data on the material’s geometry (a list of atomic nuclear positions and atomic numbers), the electron density distribution and the spin magnetisation distribution for magnetic materials. For crystals and other periodic materials, the user must also supply the periodic lattice vectors. Any quantum chemistry program can compute this data. The Chargemol program, a piece of freely-available molecular simulation software Manz developed with a colleague, reads this data and uses Manz’s new comprehensive bond order equation to calculate accurate bond orders between atoms in the material.
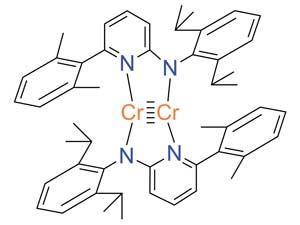
The method doesn’t work for electrides, highly time-dependent states, some extremely high-energy excited states and nuclear reactions but Manz hopes that, for everything else, it will enable chemists to compare very different materials. ‘You no longer need many different sets of rules to describe bond orders in different materials,’ says Manz. ‘Direct comparisons of bond orders become possible between small molecules, ionic materials, biomolecules, hypercoordinate molecules organometallic complexes, polymers, magnetic materials, conducting solids, semiconducting solids, insulating solids and nanostructures.’
Pavel Karen, an inorganic materials chemist at the University of Oslo, Norway, describes the new method as a black box. ‘It may just be one more in the line of previous attempts, such as the Mayer bond order from Mullikan populations or the atoms in molecules approach. For a quantum-chemical result, the bond orders exemplified in the study are not unreasonable. Just like with bond valences, the user interested must carefully consider the bonding compromises of the atoms concerned, understand their origin, and then perhaps assign the heuristic bond-order value of an integer or a fraction to the decimal result of the calculation,’ he says.
References
The paper is free to access until 13 November 2017
T A Manz, RSC Adv., 2017, 7, 45552 (DOI: 10.1039/c7ra07400j)







No comments yet