Quantum computer tackles its first triatomic

Quantum computing is extending its reach across the periodic table, with a report on calculating the energy of beryllium dihydride (BeH₂). The work, by researchers at IBM’s Yorktown Heights research centre in New York, uses a quantum computer developed at IBM with just six quantum bits (qubits).¹

Just as quantum-chemical calculations of molecules began with H₂ in 1927, studied by Walter Heitler and Fritz London, the advent of quantum computing of molecular properties also started with this simplest of molecules.² Expanding quantum computing to more complex systems containing more and bigger atoms is an important next step in developing the technology.

Conventional computers cannot model quantum systems exactly, which means they must use approximations to derive molecular properties from quantum rules. Quantum computing can dispense with these approximations because qubits can embody the quantum correlations that classical computations must break down rather crudely into single-electron wavefunctions. Yet the technique is limited to relatively simple systems because of the immense difficulty of keeping the qubits in coherent states for long enough to perform a calculation.

To simulate molecules efficiently on quantum computers, researchers have devised an algorithm called the variational quantum eigensolver (VQE), which starts with an initial guess at the answer and optimises it, a little like the classical technique of simulated annealing, but exploiting the ability of coherent qubits to encode a ‘global’ quantum state.³ Using the VQE method, researchers have previously simulated hydrogen molecules⁴ and helium hydride ions.³ 

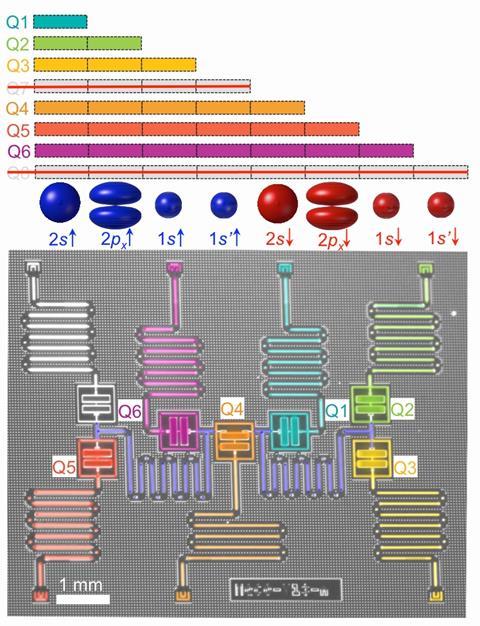
Now Jay Gambetta and coworkers at IBM have been able to use the approach to calculate the energy and bond lengths of a significantly more complex molecule, BeH₂, as well as lithium hydride LiH and a simple model of a magnetic lattice. They used a quantum computer with six qubits made from superconducting quantum interference devices (Squids) cooled to just 25mK. ‘[This work] is a significant leap forward for the quantum regime,’ says quantum chemist Markus Reiher of the Swiss Federal Institute of Technology (ETH) in Zurich.

The trick, says Gambetta, was to find a ‘trial function’ – the initial guess about the solution to the quantum equations – that makes most efficient use of the available computing resources, so that the computer can still complete the calculation during the short time that the qubits remain coherent. To calculate an observable quantity like energy, rather than the full quantum state, Gambetta says that one can get away without having to worry about correcting for errors – it’s enough just to make sure they don’t propagate too quickly. Showing the possibility of getting results for real molecules using these ‘noisy’, error-prone qubits is important, Reiher says, ‘because these are the only qubits currently available’.

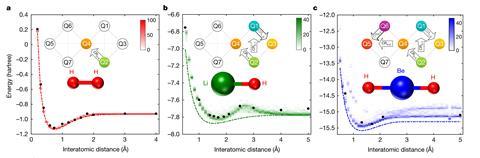
Still, he adds, calculating these properties for BeH₂ is still a ‘toy problem’. ‘In the present work, the authors could treat at most four spatial electron orbitals,’ he says. ‘Such tiny problems can be solved exactly on classical computers in almost no time.’

But, he adds, ‘as soon as one or two orders of magnitude more physical qubits becomes available – which is reachable in the very near future – the approach presented here could be applied to much larger numbers of orbitals’.